新智元报道
编辑:编辑部
让陶哲轩大神赞不绝口的形式化研究神器 Lean,运行 LLM 的推理却有个 bug。最近,加州理工团队解决了这个 bug,把 80% 以上的数学证明步骤,都自动化了!
Lean Copilot,让陶哲轩等众多数学家赞不绝口的这个形式化数学工具,又有超强进化了?
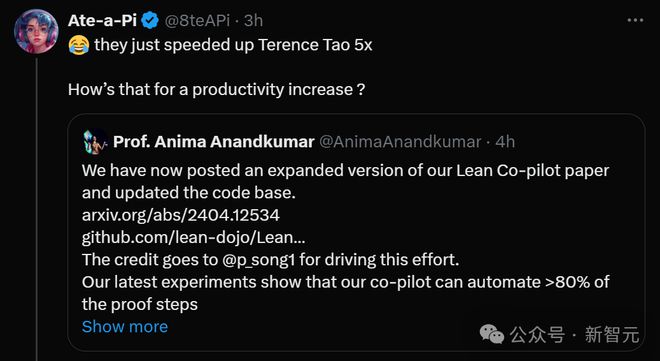
就在刚刚,加州理工教授 Anima Anandkumar 宣布,团队发布了 Lean Copilot 论文的扩展版本,并且更新了代码库。

论文地址:https://arxiv.org/pdf/2404.12534.pdf
最新实验表明,这个 Copilot 工具,可以自动化 80% 以上的数学证明步骤了!这个纪录,比以前的基线 aesop 还要好 2.3 倍。
并且,和以前一样,它在 MIT 许可下是开源的。

而对此做出巨大贡献的,是一位华人小哥宋沛洋,他是 UCSB 的荣誉 CS 本科生,加州理工学院计算+数学科学(CMS)系的 SURF 研究员。
网友惊呼:所以,陶哲轩现在的数学研究可以原地加速 5 倍了?
LLM 提出证明策略,人类无缝干预
团队就发布了这个 Lean Copilot 的工具,希望启动人类和 LLM 的协作,编写出 100% 准确的形式化数学证明。
它解决了一个核心技术挑战:在 Lean 中运行 LLM 的推理。
通过这个工具,我们就可以让 LLM 在 Lean 中提出证明策略,允许人类以无缝的方式干预和修改。
之所以开发这个项目,是因为自动化定理证明在如今仍是一项艰巨的挑战。
我们都知道,LLM 在做数学和推理任务时,时常会犯错误、产生幻觉,十分不可靠。

因此,到目前为止,数学证明大多是手动推导的,需要仔细验证。
像 Lean 这的定理证明工具,倒是可以形式化证明过程的每一步,但人类编写起 Lean,着实很费力。
在这种情况下,Lean Copilot 的诞生就显得意义重大。
让陶哲轩多次震惊的神器:数学家还不会用就完蛋了
LLM 可以作为辅助人类证明定理的工具,这一论点已经被陶哲轩多次证实了。
他前脚刚在博客里预测,26 年 AI 将和搜索、符号数学工具结合,成为数学研究中值得信赖的合著者。
紧接着,佐证他观点的研究就如雨后春笋一般源源不断地冒出来。
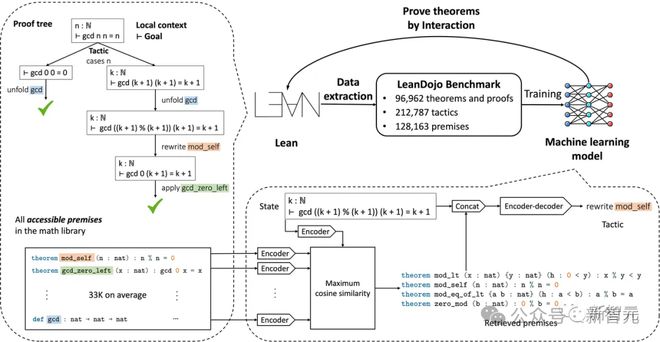
去年 6 月,加州理工、英伟达、MIT 等机构的学者,就构建了一个基于开源 LLM 的定理证明器 LeanDojo。
9 月,微软亚洲研究院、北大、北航等机构的研究人员,通过 97 个回合的「苏格拉底式」严格推理,成功让 GPT-4 得出了「P≠NP」的结论,破解了这个千禧年难题。

在第 97 轮对话中,GPT-4 得出结论,证明示例在没有穷举法的情况下无法求解,证明了结论为P≠NP
去年 10 月,陶哲轩在 GPT-4、Copilot 的帮助下,直接发现了自己论文中的一处隐藏 bug。
在用 Lean4 形式化第 6 页论点的过程中发现,他发现表达式在n=3,k=2 时,实际上是发散的。
这个不太容易看出的 bug 能被及时捉住,多亏了 Lean4。原因是,Lean 要求他构建 0 2。由此,Lean 无法基于负的0
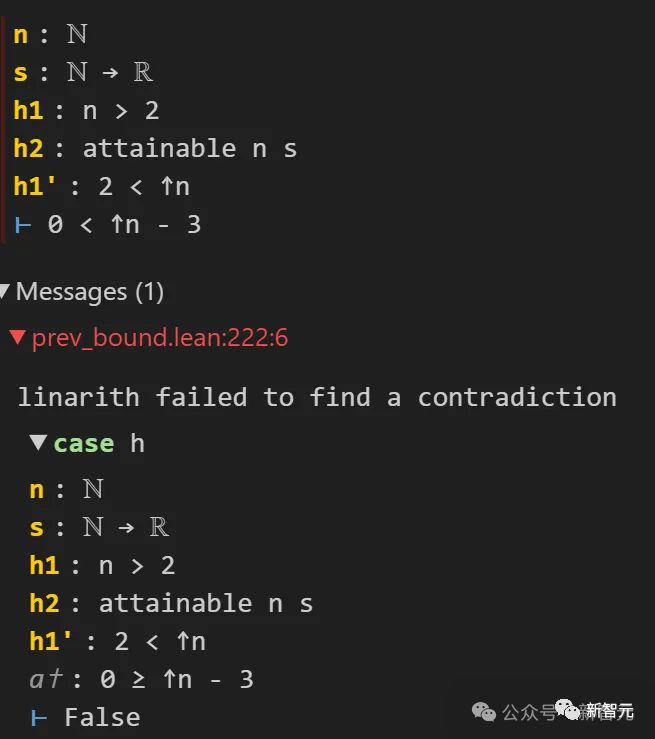
这一发现直接让陶哲轩瞳孔震惊。

而在去年年底,陶哲轩直接成功地用 AI 工具,完成了形式化多项式 Freiman-Ruzsa 猜想证明过程的工作。

最后,依赖关系图已经完全被绿色所覆盖,Lean 编译器也报告说,这个猜想完全遵循标准公理。
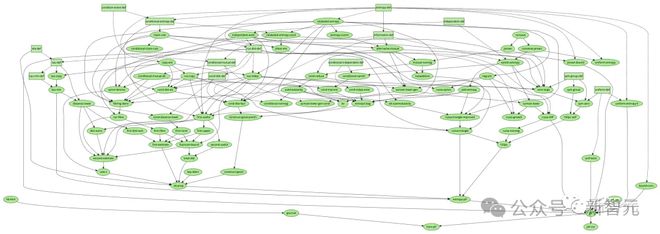
在这个过程中,所有最前线的数学研究者,都在第一时间感受到了 AI 对于数学研究颠覆力量的直接冲击。
Lean Coilot,让 Lean 更好用
而今天,Lean Copilot 的这项研究,让 Lean 直接变得更强大了。
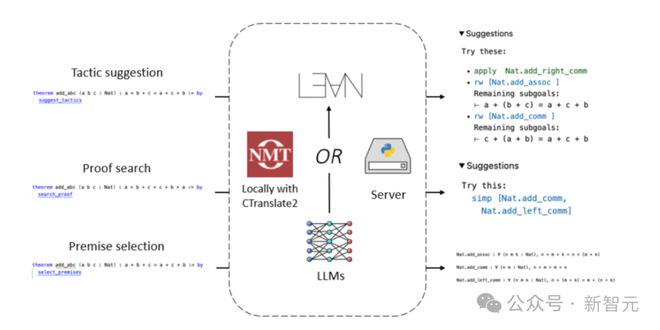
在这篇论文中,团队基于 Lean Copilot 构建了一些工具,用于建议证明步骤(策略建议)、完成中间证明目标(证明搜索)和使用 LLM 选择相关前提(前提选择)。
实验结果也充分表明了,跟 Lean 中现有的基于规则的证明自动化相比,Lean Copilot 在辅助人类自动化定理证明上,是有效的。
Lean Copilot 提供了一个通用框架,可以通过 CTranslate 2 在本地,或者在服务器上运行 LLM 的推理。
通过这个框架,用户就能创建各种自动化证明工具。
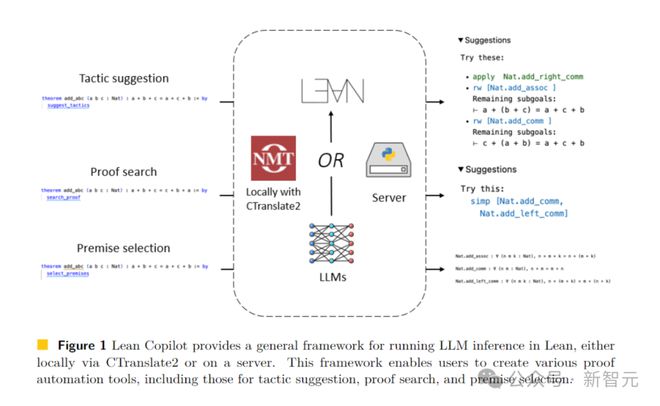
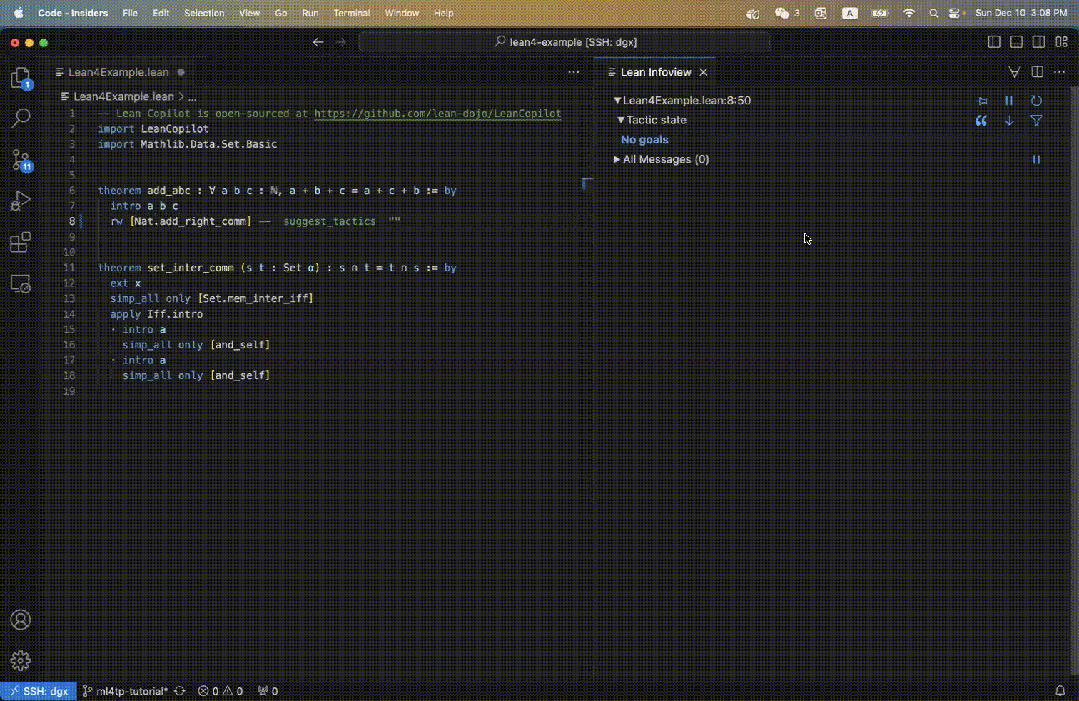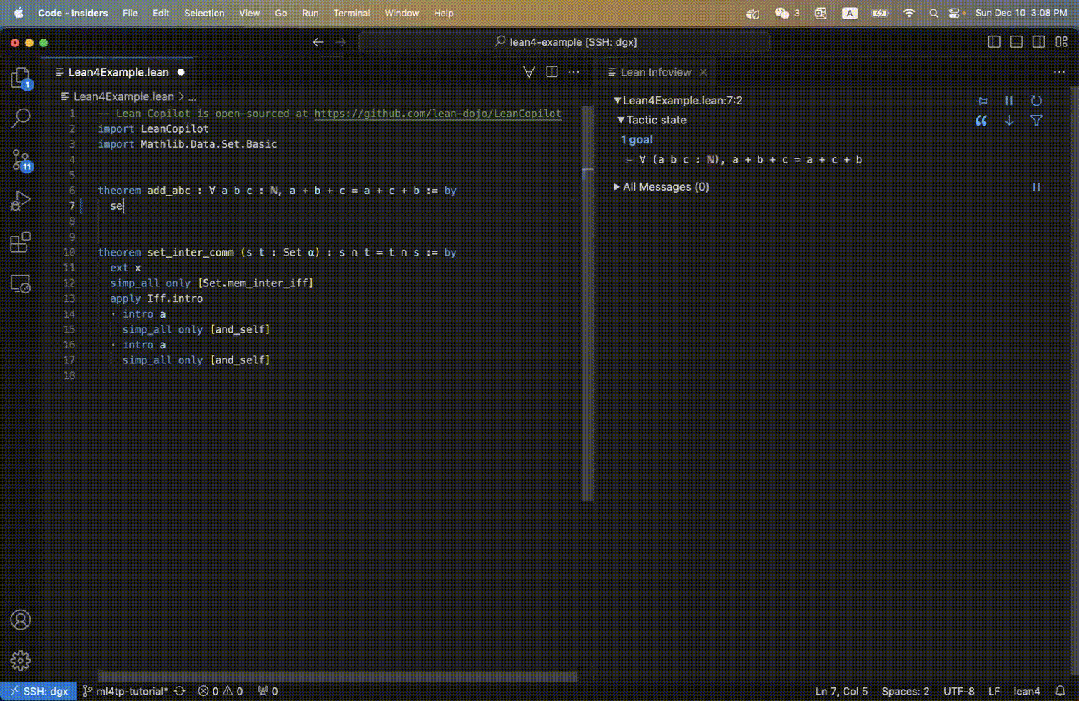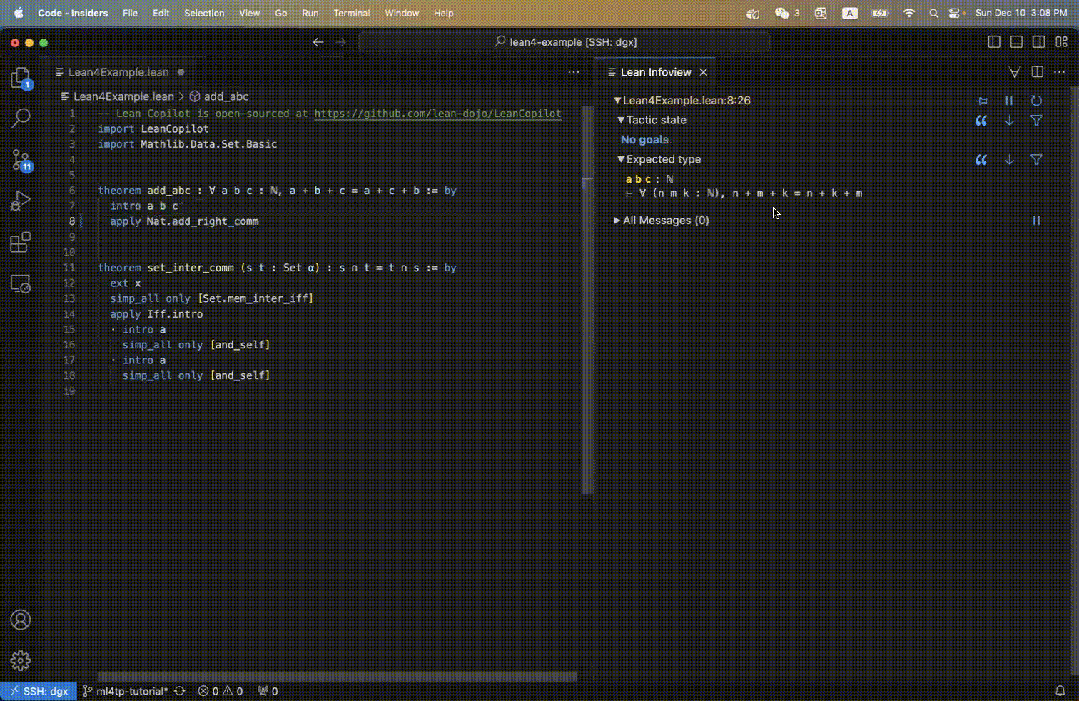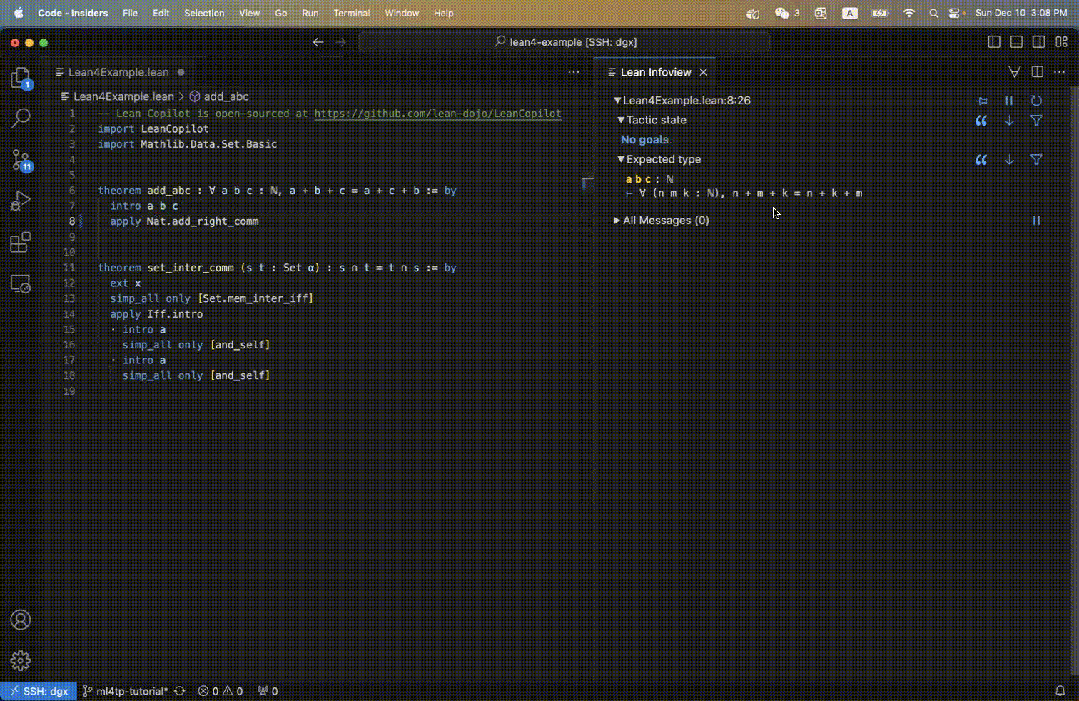
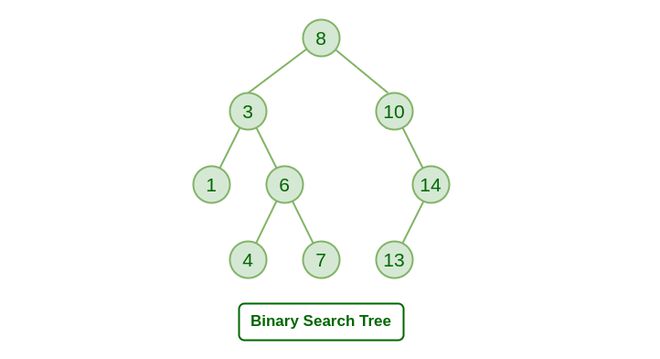
Lean 是一个在数学家中很受欢迎的证明助手。如下图所示,Lean 中的一个证明,是由一系列被称为策略(tactics)的证明步骤组成。

从整个定理开始作为初始目标,策略反复地将当前的目标转化为更简单的子目标,直到所有目标都被解决。
用户在由 VSCode 驱动的 IDE 中交互编写策略,在右边的 infoview 面板中显示目标。
生成策略建议
利用 Lean Copilot,团队构建出了 suggest_tropics,一种用 LLM 生成策略建议的工具。
而它本身,也是一种策略。
应用时,它将当前目标输入 LLM,并且从 LLM 获取生成的策略候列表。
它会查看每个选项,看它们是否会 1)导致错误;2)结果没有错,但不能完成证明;3)顺利完成证明。
如果是1),这个策略就会被删除。
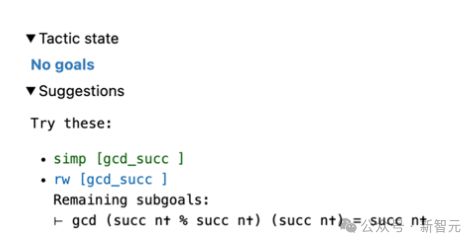
只有无错误的策略,才会显示在右边的视图面板中。
其中,成功完成证明的策略,使用绿色标记(类别3);没有错误改变证明目标,但未完成证明的策略,使用蓝色标记(类别2)。
注意!当所有列出的策略都属于类别 2 时,这个信息对于用户来说,可能极有价值。
在这种情况下,剩余目标的信息,可以直接帮助用户选择策略,作为下一个中间证明步骤。
看到建议后,用户可以选择是否接受,或使用它们作为灵感来源,制定新策略。
比如,我们在 Lean 代码中定义了一个定理 add_abc,它的初始目标如图 3 右所示。

当我们输入 suggest_tropics 时,会在右边看到策略建议。
第一个策略显示为绿色,表示证明已成功完成。
接下来三个建议均为蓝色,这就表明无法直接完成证明,但不会导致错误。
因而,它们很有可能是有效的中间证明步骤!
同时,剩余子目标也显示了出来。
而 Tactic state 字段显示 No goal,是因为至少有一个策略建议可以被证明。

搜索完整证明
此外,因为人类和机器都不能始终如一地产生正确的策略,因此在这个过程中必须回溯、探索不同的替代方案,这个过程就是证明搜索。
当是上面所说的 Suggest_tropics,仅能生成当前步骤的策略,不具备搜索多策略证明的能力。
为此,团队将其与基于规则的证明搜索工具 aesop 结合起来,构建了一个基于 LLM 的证明搜索工具。
Aesop 会将最佳优先搜索作为 Lean 的策略实施,并且允许用户配置搜索树的扩展方式。
搜索树是由作为节点的目标组成。
起初,它只有原始目标作为根节点。在每一步中,aesop 都会选择最有希望的未扩展节点,通过应用策略对其扩展,将生成的节点添加为子节点。
而当 aesop 找到一条从根源到可轻松解决的目标的路径,就证明搜索成功了!
因此,aesop 的性能关键取决于用户是否配置了有效的规则集。
这就可以看出,aesop 缺乏灵活性。因此,Search_proof 通过在每一步中由 suggest_tropics 生成的目标相关策略,来增强 aesop 的规则集,让它变得更加灵活。
对于图 3 中的原始目标,用户只需输入 search_prrof,找到可以解决目标的完整证明,就显示在了信息视图中(图 5 右)。
可以看到,由于发现了成功的证据,所以剩余的 Tactic state 是 No goals。

选择注释好的前提
此外,定理证明中另一项具有挑战性的重要任务是,找到减少或完成证明的相关前提。
除了源码库和标准库中有大量前提,Lean 还有一个大型数学库(Mathlib)。
然而,从所有库中搜索候选前提,极其困难且耗时耗力。
所以许多人都试图,能在 Lean,或其他的证明助手中得到辅助,或自动完成这一过程。

在 Lean 中,最先进的前提选择方法是,直接在 Lean 中实现的基于随机森林(random forest)的框架。
然而,前提选择任务非常适合检索增强型 LLM,即在大模型训练期间训练检索矩阵(前提嵌入),以估计证明目标与候选前提之间的相关性。
给定推理时的证明目标,首先将目标编码成一个向量,然后在前提嵌入和目标向量之间执行矩阵向量乘法。
然后,为了选择前k个前提(其中k可以是一个超参数,决定用户想要返回多少个前提),这时只需返回得分最高的k个前提。
而要在 Lean 中执行推理任务,除了 Lean Copilot 提供的快速推理外,还需要一个高效的矩阵乘法库和一个 C++ 的 numpy 矩阵阅读器。
研究人员采用了来自 CTranslate2 的矩阵乘法函数,和来自 Libnpy 的 C++ 快速 numpy 文件阅读器。
他们再次通过 FFI 机制,将这些数链接到 Lean。
因此,前提选择的策略可以非常高效地运行,因为前提嵌入可以预先计算,所有后续操作都可以使用上文介绍的库在 C++ 中快速完成。
在获得返回的前提后,研究者进一步用有用的信息对其进行注释。
这里将所有前提所分为两类:可直接在当前环境中使用的前提(范围内前提)和不可直接在当前环境中使用的前提(范围外前提)。
这取决于是否导入了所需的软件包。
如果已经导入了前提所需的包,则可以轻松使用该前提。如下图 6 显示了带注释的范围内前提。

图 7 所示是带注释的范围外前提。

下面举个使用「前提选择」的例子,对于图 3 中的定理 add_abc,可以直接在证明中输入 select_premises(图 8 左)。
然后,相关前提的列表,就会出现在信息视图中(图 8 右)。
对于这个简单的定理,可以清晰看到所选的前提确实相关,因为它们都与自然数和加法规则有关。
在这种情况下,所选的 4 个前提都在当前范围内,这意味着它们的模块已经导入。

如上,便是研究人员通过 Lean Copilot 构建的三个实用的证明自动化工具,用于策略建议、搜索证明和前提选择。
81. 2% 的证明步骤,全都自动化了
通过 Lean Copilot 框架,研究人员凭经验提出了假设——在 Lean 交互式定理证明(ITP)中进行人机协作是有益的。
由于 Lean 中的定理证明过程,主要以策略证明为主。
因此,在具体实验中,作者主要评估了用于「策略建议」,以及「证明搜索」的证明自动化工具。
总而言之,aesop 是当前是一种用于证明搜索,最先进的基于规则的证明自动化工具。
研究人员在两种情况下,验证了基于 LLM 的搜索证明与 aesop 相比的有效性:
(1)自主证明定理(LLM 独立完成)
(2)协助人类进行定理证明(人类与 AI 协作)
此外,研究者还将搜索证明与策略建议进行了比较,以证明除了单一策略建议之外,搜索证明体现的优势。
研究 Lean Copilot 如何有效地帮助人类进行 ITP 的过程,类似于人类在软件编程中使用 Copilot 的范式。
也就是说,当我们面对一个目标时,首先会调用 Copilot,看其是否可以直接解决问题。
如果不能,我们会进一步简化目标,然后再次尝试 Copilot。然后,一直重复上述过程,直至 Copilot 成功解决剩余目标。
而研究人员便是通过这样的迭代协作范例中,去查看每个证明自动化工具可以自动化多少人力。
具体结果,如下表 1 显示。
证明搜索(search_proof)可以自动证明 64% 的定理(50 个中的 32 个),明显高于 aesop 和策略建议(suggest_tropics)。
当用于辅助人类时, 证明搜索仅需要平均 1.02 个手动输入策略,这也比 aesop(3.62)和策略建议(2.72)更好。

最后,对于每个测试的定理,作者计算了三个工具中每一个可以自动化的证明步骤的百分比。
结果发现,证明搜索可以自动完成定理中约 81.2% 的证明步骤,明显高于策略建议(48.6%)和 aesop(35.2%)。
总之,证明搜索的性能比策略建议,要高出 1.67 倍,比基于规则的基线 aesop 高 2.31 倍。
通过 Copilot 在 Lean 中进行本地 LLM 推理
Lean Copilot 中的 tactic 建议、证明搜索和前提选择,这三个任务在本质上可能看起来不同,但对于用户体验的要求是相似的。
它们都需要足够快速地生成响应,具有适中的计算需求,同时在 Lean 中运行。
用户之所以有这些要求,是因为 Lean 本身在大多数情况下都能非常快速地提供环境反馈(比如剩余目标,错误信息,类型信息等)。
这种快速,跟证明定理的本质是一致的——它需要连贯的推理。
如果 Lean Copilot 需要用户等待很长一段时间,那么人类和 AI 之间的协作就很难发挥作用。
同样,我们也非常希望满足低计算的需求。因为 Lean 中的定理证明本身不需要 GPU,可以在用户本地的笔记本电脑上运行。
因此,能够在大多数硬件(包括没有 GPU 的笔记本电脑)上高效运行,对于 Lean 的用户就非常重要。
因为用户在编写证明时,可能无法访问支持 CUDA 的 GPU。
因为需要满足快速推理和低计算需求,而且所有流行的高效深度学习框架都是在 Python 中,团队想到的一个自然的解决方案,就是在 Python 中托管模型(本地或远程),然后从 Lean 向模型发出请求。
然而,这种方法会受到进程间通信的开销的影响,并且它需要用户执行额外的设置步骤,并不适合 Lean 的传统工作流程。
为了克服这些问题,Lean Copilot 通过外部功能接口(FFI)在 Lean 中本地运行 LLM。
FFI 是一种机制,可以用一种语言编写的程序调用另一种语言的子程序。
Lean 部分用c++实现,可以与c++高效互操作。
程序员可以在 Lean 中声明一个函数,但在c++中实现函数体。实现会被编译到一个共享库中,并动态链接到 Lean。
默认情况下,我们采用的是 LeanDojo 预训练的 repver 模型。它基于一个编码器-解码器转换器,BVT5,它将输入字符串映射到输出字符串。
Lean Copilot 通过将模型包装成一个对字符串操作的c++函数,使其在 Lean 中可运行,该函数可以通过 FFI 在精益中调用。
华人作者立大功
最新论文中的三人团队,也是 23 年 6 月开源平台 LeanDojo 其中的作者。

论文地址:https://arxiv.org/pdf/2306.15626.pdf
Peiyang Song(宋沛洋)

宋沛洋是加州大学圣巴巴拉分校创意研究学院(CCS)的计算机科学荣誉本科生,导师是 Richert Wang 和 Phill Conrad 。
与此同时,他还是加州理工学院计算与数学科学系(CMS)的 SURF 研究员,由 Anima Anandkumar 教授和 Kaiyu Yang 博士共同指导。
另外,他还是 UC 伯克利建筑实验室的研究员,与 Tim Sherwood 和 Dr. Jeremy Lau(谷歌)一起合作。
他的研究兴趣是机器学习(ML),涉及自然语言处理(NLP)和计算机视觉(CV)等应用领域,以及系统和编程语言(PL)等基础理论。
宋沛洋最近的研究主要有两个方向。
一是神经符号推理和人工智能数学(AI4Math),将大模型与交互式定理证明器(ITPs)相结。
另一个是基于时序逻辑的高能效机器学习。
Kaiyu Yang(杨凯峪)

杨凯峪是加州理工学院计算+数学科学(CMS)系的博士后研究员,导师是 Anima Anandkumar。
他曾在普林斯顿大学获得了博士学位,导师是 Jia Deng,还曾与 Olga Russakovsky、陈丹琦一起工作。
他的研究重点是神经符号人工智能,旨在使机器学习能够进行符号推理,希望通过两个方向实现:
(1)将机器学习应用于符号推理任务,如形式逻辑或自然语言中的数学推理和定理证明;
(2)将符号组件引入机器学习模型,使其更具可解释性、可验证性和数据高效。
目前,他正在研究能够理解和推理数学的人工智能。数学推理是人类智能的一个重要里程碑,它有可能改变科学和工程中的许多重要问题,比如解决偏微分方程和公式验证。
Anima Anandkumar

Anima Anandkumar 现在是加州理工学院计算和数学科学教授。
她的研究兴趣主要集中在大规模机器学习、非凸优化和高维统计等领域。
特别是,她一直在带头开发和分析机器学习的张量算法。
张量分解方法具有极高的并行性和可扩展性,可应用于海量数据。它可以保证收敛到最优解,并对许多概率模型(比如 Markov 模型)输出一致的估计结果。
更广泛地说,Anandkumar 教授一直在研究加速非凸优化的高效技术。
参考资料:
https://arxiv.org/abs/2404.12534
https://github.com/lean-dojo/LeanCopilot
https://twitter.com/AnimaAnandkumar/status/1782518528098353535