新智元报道
编辑:Aeneas 好困
困扰全世界几个世纪的「臭名昭著」谜题——费马大定理,或将被 AI 攻克?一位英国数学家宣布,即将启动用 Lean 重现费马大定理证明过程的项目,将 100 页证明变成代码。从此,世界顶尖数学难题的证明将成为「众包」项目,你我都可以进去添几笔。
费马大定理,即将被 AI 攻克?
而且整件事最意味深长的地方在于,AI 即将解决的费马大定理,正是为了证明 AI 无用。
曾经,数学属于纯粹的人类智力王国;如今,这片疆土正被先进的算法所破译,所践踏。

费马大定理,是一个「臭名昭著」的谜题,在几个世纪以来,一直困扰着数学家们。
它在 1993 年被证明,而现在,数学家们有一个伟大计划:用计算机把证明过程重现。
他们希望在这个版本的证明中,如果有任何逻辑上的错误,都可由计算机检查出来。
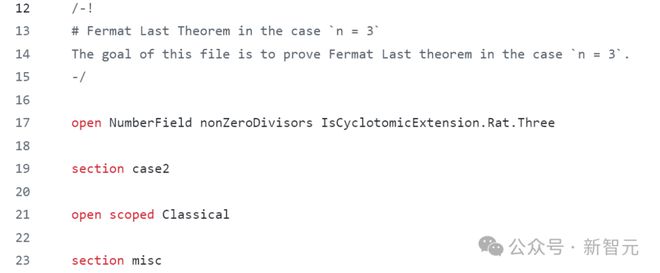
项目地址:https://github.com/riccardobrasca/flt3
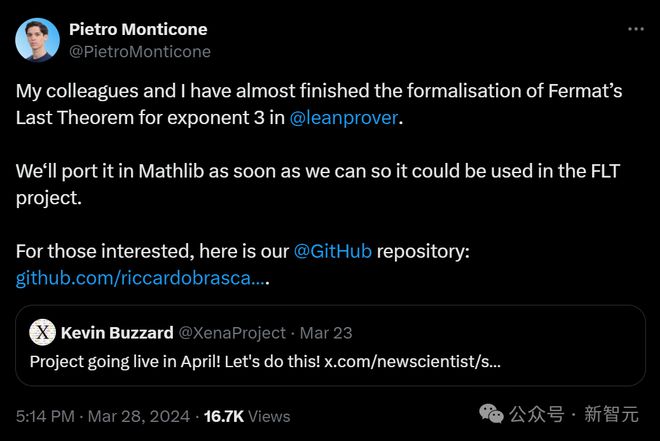
3 月底,数学家 Pietro Monticone 激动地表示,自己和同事几乎在 leanprover 中完成了指数 3 的费马大定理的形式化。
他们会尽快把形式化过程移植到 Mathlib 中,以便在 FLT 项目中使用。
证明过程大致遵循 Wiles 的证明,但会略有改动。
用 Lean 把费马大定理变成代码
当四月到来时,数学家兼程序员 Kevin Buzzard 将发布这个计划:通过计算机代码,完成费马大定理的证明。
项目在 4 月上线后,公开的蓝图就会出现在网上,届时,Lean 社区的任何人,都可以为形式化证明做出自己的贡献。

把一个开创性的 100 页数学证明,变成计算机代码,这个过程容易实现吗?
这当然就要归功于被陶哲轩大加赞赏、沉迷使用的证明工具 Lean,它可以让用户把散文式的证明转化为用于测试的规则和逻辑。

但无论如何,这项工程都不简单,预计将历时多年,而 Kevin Buzzard 页获得了项目的资金支持。
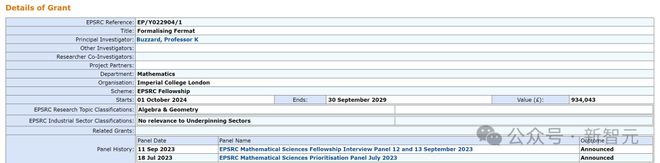
大家都明白,这个项目,很可能是迄今为止最复杂的计算机化方式证明之一。

费马大定理
费马大定理,堪称是史上最精彩的一个数学谜题。
而证明费马大定理的过程,直接就是一部数学史。

我们耳熟能详的费马大定理,由 17 世纪的法国数学家皮埃尔·德·费马提出。遗憾的是,他未能在有生之年找到证明。
于是,这项起源于三百多年前的难题,直接挑战了人类整整 3 个世纪,多次震惊全世界,耗尽人类众多最杰出大脑的精力,也让千千万万业余者痴迷。

这个定理声称,不存在三个正整数a、b、c能满足方程 (a^n + b^n = c^n),其中n是任何大于 2 的整数。
这个证明的难点就在于,数学家很难找出一个否定案例:我们怎么能保证一定不存在这样一个无穷大的整数n,能满足这个方程式呢?

幸好,对于今天的数学家来说,将无穷大的概念转换成逻辑,并不是什么新鲜事了。
在较为简单的证明中,我们可以依靠归纳法——
一旦某个逻辑对某个数字成立(比如8),那么它对于之后的每一个数(比如9、10、11 等)都同样成立,直到无限大。
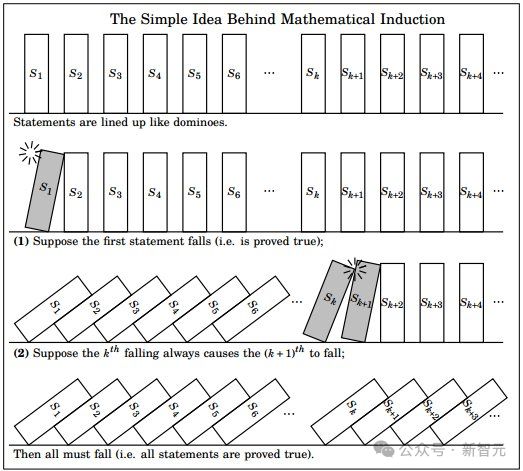
然而,费马大定理却是数学界百年来的一块绊脚石。
直到 1993 年,英国数学家 Andrew Wiles 用一份长达 100 页的书面证明,解开了这一谜团。

计算机为什么无法证明费马大定理?
业界认为原因有三:
1. 计算机无法推导出无穷种
2. 计算机无法证明逻辑正确
3. 计算机可能会出现转瞬即逝的失误
幸好有 Lean 辅助证明
一份 100 页的数学证明,无论是对于普通的数学系学生,还是数学家,都不是那么好驾驭的。
好在,我们可以不再依赖传统的证明方法,可以求助于 Lean 这样的工具。
它是一款基于 C++ 开发的编程工具,专为编写和验证归纳法证明而设计。
如今许多所谓的「人工智能」,不过是巧妙地排列模仿人类语言的文字。但 Lean 这类计算机辅助的证明,更深入地融合了人类的思维方式,和计算机辅助加强的能力。
Lean 编程工具,进入本科课堂
在伦敦帝国理工学院教数学的 Kevin Buzzard,花费了数年时间,利用 Lean 为学院的整个本科数学课程开发了支持工具。
通过这些工具,学生们可以将课堂上讨论的内容分解成逻辑和数学运算的步骤。
这就仿佛是一个数学证明上的罗塞塔石碑。
同为数学教师的 Clarissa Littler,就非常赞同 Kevin Buzzard 的理念。
她在波特兰社区学院教授离散数学。过去两个学期里,她都在离散数学课上用 Kevin Buzzard 开发的「Lean 经典入门游戏」。

她会用「自然数博弈」,帮学生熟悉数学归纳法的思想,通过「集合论博弈」,让他们习惯于对集合进行推理。
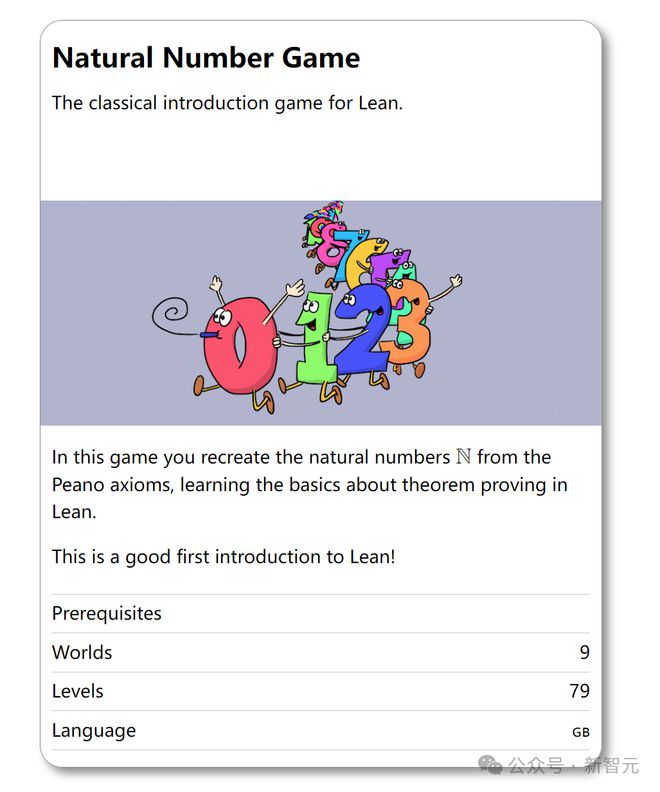
在这个过程中,学生们对「严格遵循逻辑规则编写证明」,和「用通俗语言解释事物真理」之间的理解差距,就会逐渐弥合。
Littler 强调,课程的一大重点,就是让数学基础不太牢固的学生,更自如地用数学家的方式思考,同时更好地理解证明、证据和展示真理的方法。
这种从形式逻辑到规则列表,再到用散文表达的转变,是将项目分解成互相协作的代码片段的关键所在。
而这一点,在编程和纯数学的交叉领域尤为重要,也正是 Lean 这样的工具能大放异彩的地方。
Buzzard 表示,他希望将费马大定理引发的复杂数学思想转化为可编程的形式。
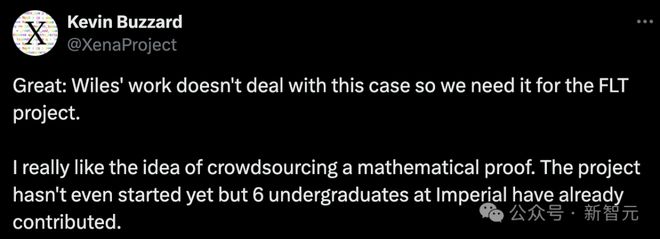
几个世纪以来,为了证明这个在 Buzzard 看来「毫无实际意义」的定理,人们开创了许多极具价值的新数学分支。
是的,在 Buzzard 看来,费马大定理毫无意义,在现实世界中没有任何应用,不过因为这个「臭名昭著」的问题,几个实际来人们产生了大量绝妙的新想法。
如今,将 Wiles 的 100 页长的证明转化为计算机能够理解的形式语言和规则,有望为新一代数学家开启计算机辅助证明的大门。
而这种转换工具,也能够为编程人员提供帮助。
Littler 表示,在这一领域,雄心勃勃的项目总是值得尝试的,因为我们都能从学到的经验和编写的程序库中获益。
交互式的定理证明虽然还是一个较新的领域,但 Lean 社区已经做了许多优秀的工作。
Kevin Buzzard:Lean 的布道者
1968 年出生的 Kevin Mark Buzzard,在算术几何和 Langlands 程序方面有着深厚的专业造诣。
他目前是伦敦帝国学院的纯数学教授,也是 AI 工具 Lean 的「布道者」。
在皇家文法学校读书期间,Kevin Buzzard 曾参加了国际数学奥林匹克竞赛,并在 1986 年赢得铜牌,1987 年以满分拿下金牌。

此后,他在剑桥大学的三一学院完成了数学本科学习,并于 1990 年获得 Senior Wrangler 头衔,于 1991 年获得C.A.S.M.学位。
在 Richard Taylor 的指导下,他的博士论文「The levels of modular representations」于 1995 年完成,探讨了数学中的一个复杂领域。

1998 年,他开始在伦敦帝国学院担任讲师,2002 年晋升为高级讲师,2004 年被任命为教授。
他还曾在哈佛大学(2002 年 10 月至 12 月)和其他几所著名机构进行访问研究。
因其在数论领域的突出贡献,他在 2002 年获得了怀特黑德奖,2008 年获得了 Senior Berwick 奖。
2017 年,Buzzard 发起了一个关于 Lean 定理证明器的项目和博客,致力于推动在数学研究中使用计算机辅助证明工具。
他还指导了音乐家 Dan Snaith(艺名 Caribou)完成了关于超收敛 Siegel 模符号研究的数学博士论文,Snaith 因此从伦敦帝国学院获得了博士学位。
2023 年 10 月,Kevin Buzzard 在社交媒体上称,自己获得了研究经费,开始用 Lean 去证明费马大定理。
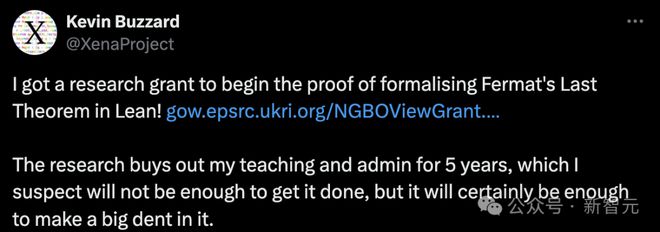
Buzzard 表示,「十年前,这需要花费无限多的时间」。为了完成这个项目,他将把自己的教学任务搁置五年。
搁置自己的任务,值得吗?
在他的同行、英国诺丁汉大学 Chris Williams 看来,这种项目可能会产生意想不到的好处,和深远的影响。
「我认为他不太可能在未来五年内正式形式化整个证明,否则就太惊人了。但是,现在的数论和算术几何中,许多工具都无处不在,因此我预计,未来任何实质性的进展都将非常有用。」
对数学研究意义重大
这个项目还揭示了一个更深层次的价值。
随着计算工具的不断进步,数学的不同分支之间,甚至不同学科之间的界限,正变得越来越模糊,这就导致一些几乎无法验证的证明出现了。
比如,京都大学的日本数学家 Mochizuki Shinichi 编写了一份长达 500 页的证明,因为太过复杂,花费了数年时间才发表出来,部分原因就是,人们不知道该如何处理它。
从此,我们可能会发现,数学的边界变得越来越模糊。
这不是指真实性或逻辑上的模糊,而是指一个证明中可以融合的不同思想的范围。
Lean 可以让数学家们的思想转化为代码,这就让同行更易于理解。看着前人记录的先例,未来的数学家们可以在此基础上继续推进自己的研究。
Buzzard 表示,用 Lean 进行数学写作的特点就是,你可以留下精确陈述但未经证明的结果,而其他人就可以在之后解决它们。
Lean 本身就促成了这样一种工作流。
换言之,费马大定理正准备以「众包」的方式来解决——特别是如果编码工作超出了 Buzzard 剩余的工作年限。
完成一个数学证明需要整个社区的努力。
也许,在将来,我们能拥有一个类似 Genius.com 的平台,用于分享和解读数学证明。
参考资料: